25 Сжатие информации. Основные алгоритмы сжатия: Хафменна, RLE, LZ77

Алгоритм RLE

В основу алгоритмов RLE положен принцип выявления повторяющихся последовательностей данных и замены их простой структурой, в которой указывается код данных и коэффициент повтора.

Например, для последовательности: 
0; 0; 0; 127; 127; 0; 255; 255; 255; 255 (всего 10 байтов)          
образуется следующий вектор, который при записи в строку имеет вид:    
0; 3; 127; 2; 0; 1; 255; 4 (всего 8 байтов). 

В данном примере коэффициент сжатия равен 8/10 (80 %).

Программные реализации алгоритмов RLE отличаются простотой, высокой скоростью работы, но в среднем обеспечивают недостаточное сжатие. Наилучшими объектами для данного алгоритма являются графические файлы, в которых большие одноцветные участки изображения кодируются длинными последовательностями одинаковых байтов. Этот метод также может давать заметный выигрыш на некоторых типах файлов баз данных, имеющих таблицы с фиксированной длиной полей. Для текстовых данных методы RLE, как правило, неэффективны.

 

Алгоритм Хаффмана

Алгоритм основан на том факте, что некоторые символы из стандартного 256-символьного набора в произвольном тексте могут встречаться чаще среднего периода повтора, а другие, соответственно, – реже. Следовательно, если для записи распространенных символов использовать короткие последовательности бит, длиной меньше 8, а для записи редких символов – длинные, то суммарный объем файла уменьшится.

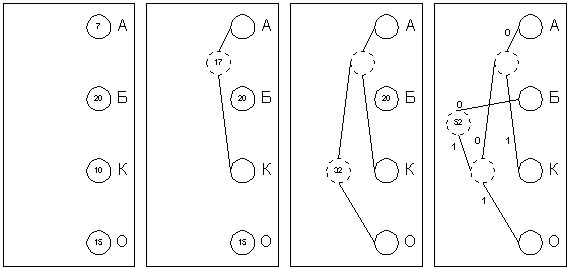
Хаффман предложил очень простой алгоритм определения того, какой символ необходимо кодировать каким кодом для получения файла с длиной, очень близкой к его энтропии (то есть информационной насыщенности). Пусть у нас имеется список всех символов, встречающихся в исходном тексте, причем известно количество появлений каждого символа в нем. Выпишем их вертикально в ряд в виде ячеек будущего графа по правому краю листа (рис. 1а). Выберем два символа с наименьшим количеством повторений в тексте (если три или большее число символов имеют одинаковые значения, выбираем любые два из них). Проведем от них линии влево к новой вершине графа и запишем в нее значение, равное сумме частот повторения каждого из объединяемых символов (рис.2б). Отныне не будем принимать во внимание при поиске наименьших частот повторения два объединенных узла (для этого сотрем числа в этих двух вершинах), но будем рассматривать новую вершину как полноценную ячейку с частотой появления, равной сумме частот появления двух соединившихся вершин. Будем повторять операцию объединения вершин до тех пор, пока не придем к одной вершине с числом (рис.2в и 2г). Для проверки: очевидно, что в ней будет записана длина кодируемого файла. Теперь расставим на двух ребрах графа, исходящих из каждой вершины, биты 0 и 1 произвольно – например, на каждом верхнем ребре 0, а на каждом нижнем – 1. Теперь для определения кода каждой конкретной буквы необходимо просто пройти от вершины дерева до нее, выписывая нули и единицы по маршруту следования. Для рисунка 4.5 символ "А" получает код "000", символ "Б" – код "01", символ "К" – код "001", а символ "О" – код "1".

Код Хаффмана является префиксным, то есть код никакого символа не является началом кода какого-либо другого символа. Проверьте это на нашем примере. А из этого следует, что код Хаффмана однозначно восстановим получателем, даже если не сообщается длина кода каждого переданного символа. Получателю пересылают только дерево Хаффмана в компактном виде, а затем входная последовательность кодов символов декодируется им самостоятельно без какой-либо дополнительной информации. Например, при приеме "0100010100001" им сначала отделяется первый символ "Б" : "01-00010100001", затем снова начиная с вершины дерева – "А" "01-000-10100001", затем аналогично декодируется вся запись "01-000-1-01-000-01" "БАОБАБ".

 

Семейство алгоритмов LZ77.

Алгоритмы семейства LZ77 довольно просты в реализации. Поэтому именно они широко используются в популярных архиваторах. Эффект сжатия у этих алгоритмов достигается за счет замены уже встречавшихся ранее в тексте фраз на пару значений (ссылка назад, длина фрагмента). Все алгоритмы этого семейства отличаются друг от друга размером окна обзора предыдущего текста и максимальным и минимальным размером заменяемого фрагмента. От выбора этих параметров существенным образом зависит быстродействие конкретной реализации алгоритма.